"Chapter. 0 - 함수의 연속"
게시글 주소: https://test.orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

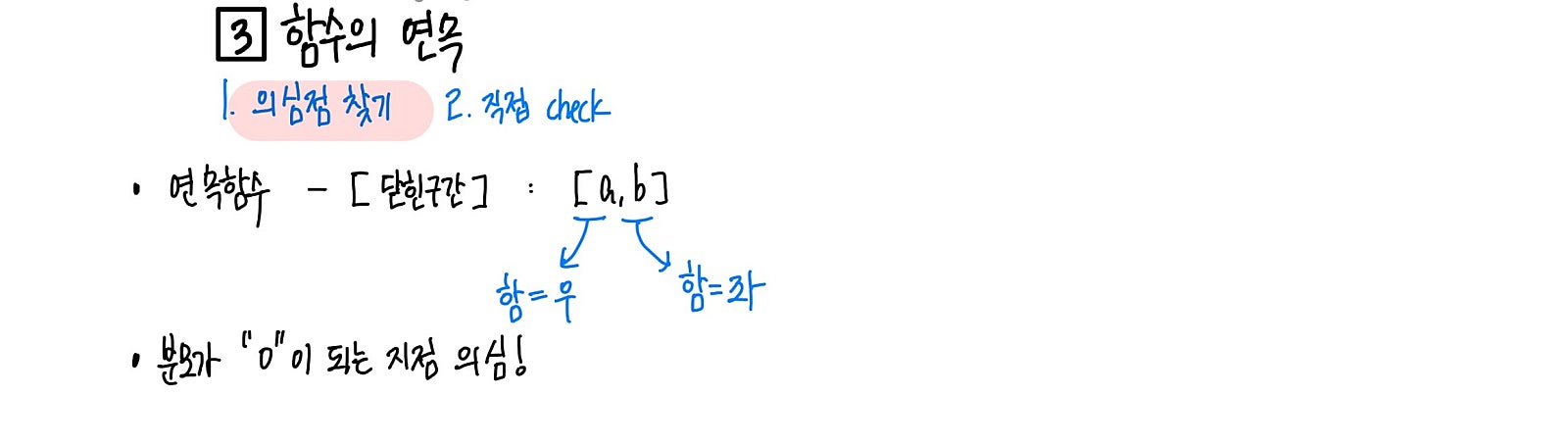
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
중대글로벌금융점공좀보여주실분있으실까요 부탁드립니다!!
-
90은 어케하는거 대체
-
너무 진지하게 하지말기 오르비 칼럼이나 재밌는 신문 하나 읽는다고 생각하기 힘빼기...
-
추합 조기발표는 0
가능성이,,, 없는거겠죵
-
글이 완전히 안 읽히네요.. 가능세계 지문 푸는데 첫문제만 맞고 다 틀림 ㅋㅋ
-
그래서 하루종일 쳐 노는중
-
돈 개많이 들던데
-
평가원 #~#
-
?
-
생윤 김종익쌤 ebs 2020꺼만 있던데 걍 저거 들어도 괜찮을까요 0
찾아보니까 김종익쌤 추천 많이 하셔서요
-
❤️서강대학교 자연과학대학 (수학과, 물리학과, 화학과, 생명과학과, SCIENCE...
-
안과가야겠다
-
니혼은 뭔가 뭔가인데
-
승무원이 안전벨트 다메 라고해서
-
윾넨이에 검색해도 경제 독서 지문만 존나 나왔음
-
옯평 21
존나 높네요… 얼굴이든 지능이든… 신은 불공평해
-
반쯤 붙었다 해도 되는 부분?
-
어떤 편인가요 지금 풀고 있는데 빡세길래 다들 느끼는 체감난도는 어떠신지 궁금합니다
-
기분이 좀 우울하고그래 나도 할머니댁가고싶은데 ㅠ
-
씻고 다시 리츄라이 13
on
-
연애하고싶네 3
우웅...
-
왜 왜 왜
-
테세우스의 배 5
굉장히 흥미롭네요
-
수능 수학으로 치면 무등비 삼도극 같은 기출이 많아요 하자니 어차피 95% 확률로...
-
낼까지 70찍어보겠습니다
-
얼버기 13
-
착한오르비언 특) 20
팜하니 20렙 달성 축하해줌.
-
진짜 하나도 모르는 쌩노베가 1년 빡세게해서 1맞기 가능?
-
뭐요
-
부산에서 경기도 올라가자마자 눈구경 하긴 하는데 이정도로 바라진 않았어..
-
인증해달란 나쁜말은 ㄴㄴㄴㄴㄴㄴ.
-
김승리 유대종 3
오리진은 완강했고..올오카를 듣는중인데 문학이 안 맞는 감이 있어서 유대종t 문학...
-
갑자기 막 3
옷을 벗고싶은데 이거 이상한가요 후하후하
-
오십에 읽는 주역 강기진 명언 명대사 인상깊은 책 구절 글귀 0
오십에 읽는 주역 강기진 명언 명대사 인상깊은 책 구절 글귀이 책의 가장 인상적인...
-
국어 3등급인데 6
6,9평 비문학 다 맞고 문학 많이 틀려서 비문학 잘하고 문학을 못하는 줄 알았는데...
-
6번까지는 도나요? 젭알...
-
2H(5n-2x-2)라 간단할 것 같은데 아님말고..
-
왜 남녀구조는 3
거의 남자가 더 고백하고 남자가 더 적극적이어야할까 대부분 남자가 더 적극적이잖음
-
이런 사진 보면 12
숨이 갑갑해지는데 백룸 혐오체질인듯 사진은 시대인재 기숙입니다
-
수능 어렵고쉽고 문제가아니고 간단함 걍 학령인구가 줄어들고있기때문. 맞음?
-
ㅇㅈ 5
약 1시간 전
-
사문은 무조건할껀데 생윤은 현역 반수 둘다 4등급 나왔음 (모고때는 1~2...
-
조언 구합니다 2
고3 된 외고생입니다 조언을 받을 사람이 없어서 글을 썼습니다. 제 친구가...
-
ㅇㅈ 1
스키장 옴 재밌어
-
발표났다고 문자오나요???
-
몸무게는 벌써 명절을 보냈구나..
-
하....
-
전화 못받으면 어케됨…?….. 글구 합격증 못받음요????













































