[과천중앙고] 1학년 2학기 기말고사 고난도 문항 손풀이
게시글 주소: https://test.orbi.kr/00065860174
안녕하세요. 어수강 박사입니다.
오늘은 "[과천중앙고] 2023년 1학년 2학기 기말고사 고난도 문항 손풀이를 포스팅" 하도록 하겠습니다.
먼저 17번 문항입니다.
박스의 두 번째 조건을 기준으로 경우 나누기를 하면 되겠죠? 이후 박스의 첫 번째 조건과 세 번째 조건을 만족하는지 확인하면 될 것 같네요. 구체적인 풀이는 다음과 같습니다!
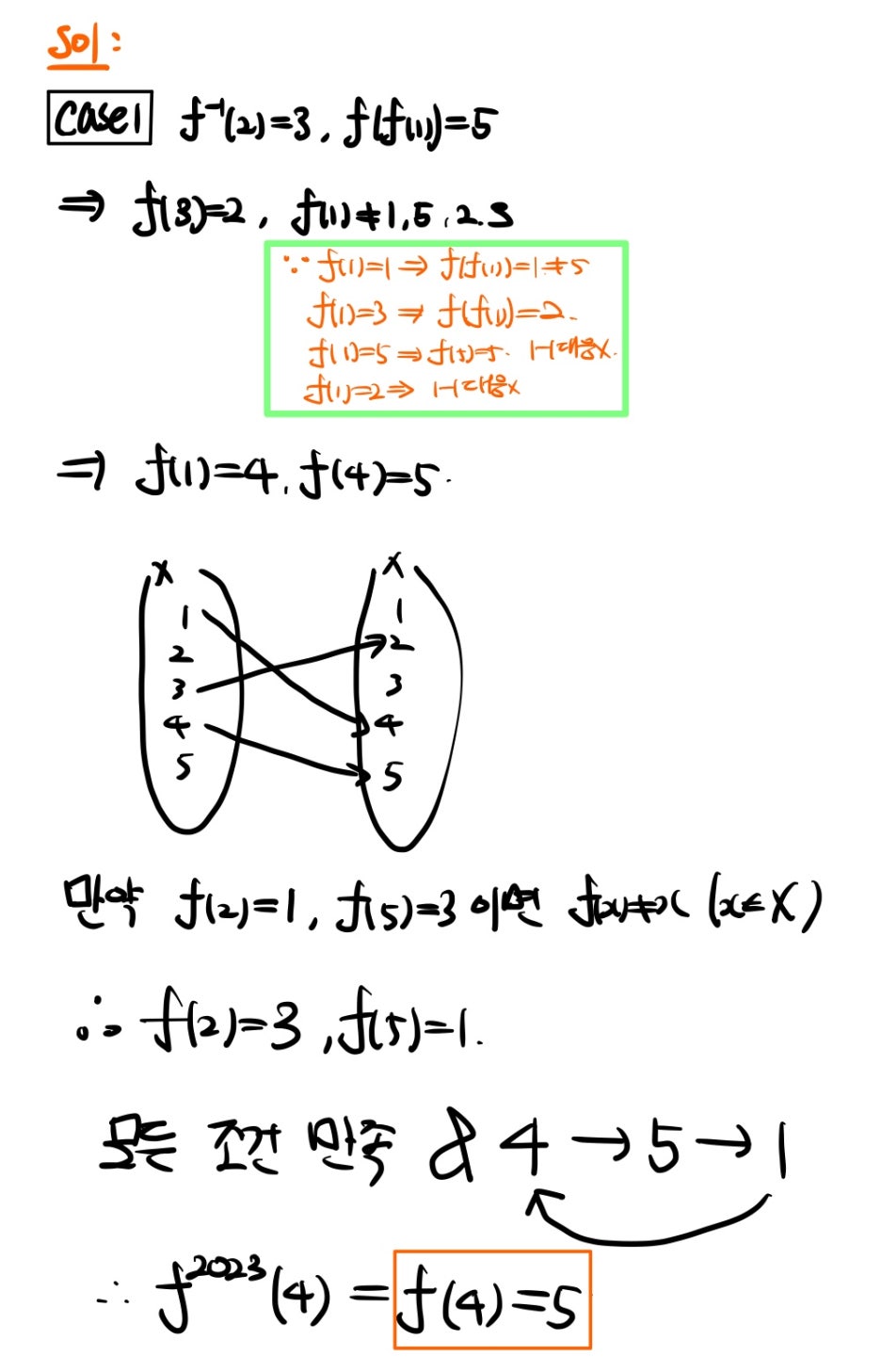
별로 어렵지 않죠? 답은 나왔지만~ Case2도 마저 생각해 볼게요!
(시험에서 case1, case2의 순서가 뒤바뀔 수도 있으니까요 ㅎㅎ)
.
다음은 18번 문항입니다.
대수적으로 풀기 어렵다면 기하적으로 풀면 되겠죠? 함수 y=f(x)의 개형을 그리는 것으로 시작하면 될 것 같습니다.
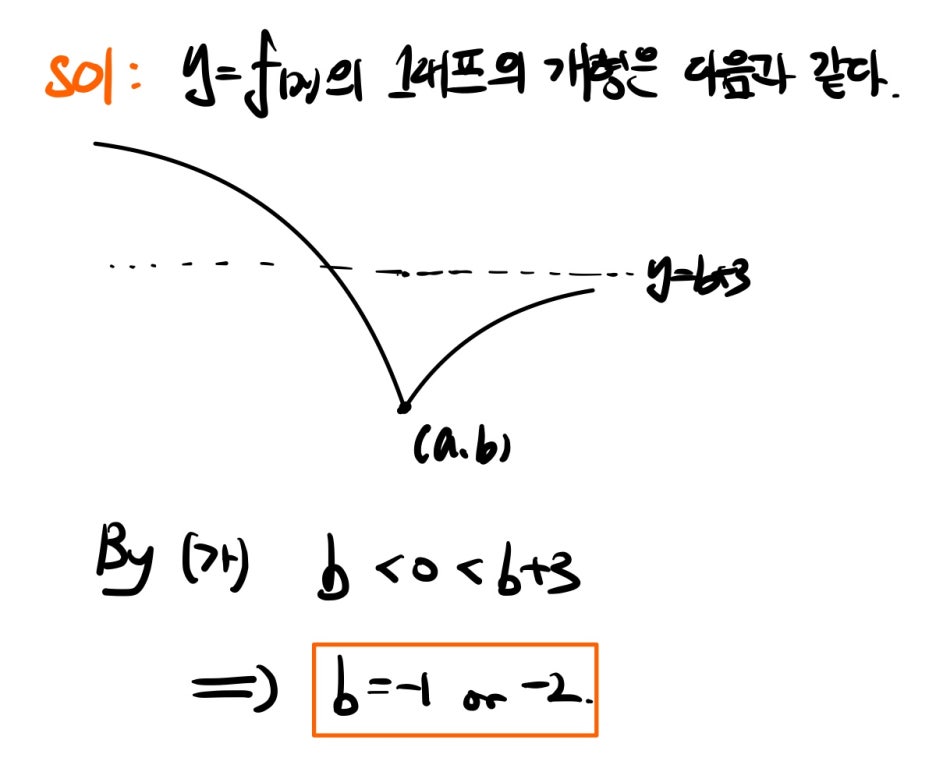
이제 b의 값에 따라 경우를 나누어 풀면 되겠네요! ㅎㅎ 먼저 b=-1인 경우는 다음과 같습니다.
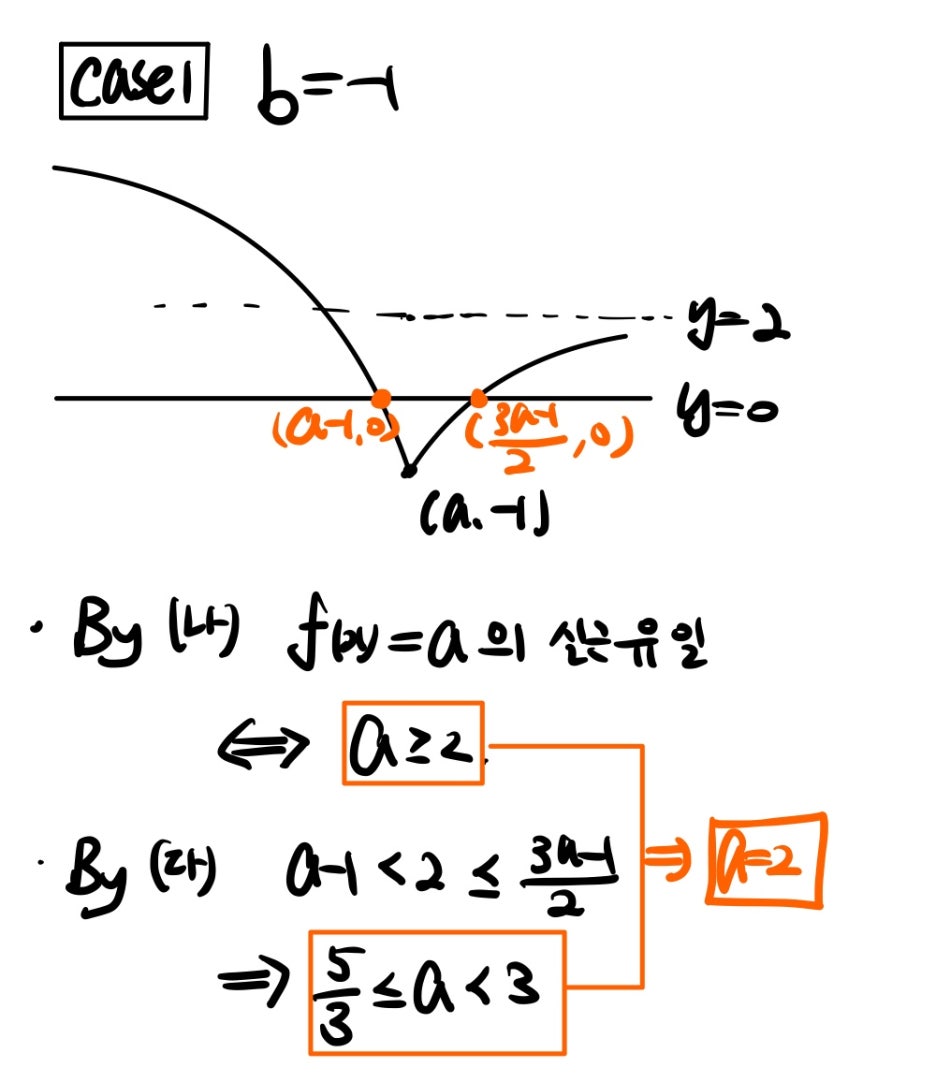
이제 b=-2인 경우만 생각하면 되겠죠?
따라서 답은 다음과 같습니다.
마지막으로 논술형 4번입니다.
복잡해 보이지만 차근차근 풀면 별 거 아니니 쫄지 마세요!ㅎㅎ
저는 조건 (가), (라), (나) 순으로 풀었지만, 순서는 별로 중요하지 않습니다. 하나하나 차근차근 풀기만 하면 됩니다!
저의 풀이는 다음과 같습니다. (참고로 조건 (다)는 쓸모가 없습니다. 왜 저런 조건을 줬을까요?^^;;)
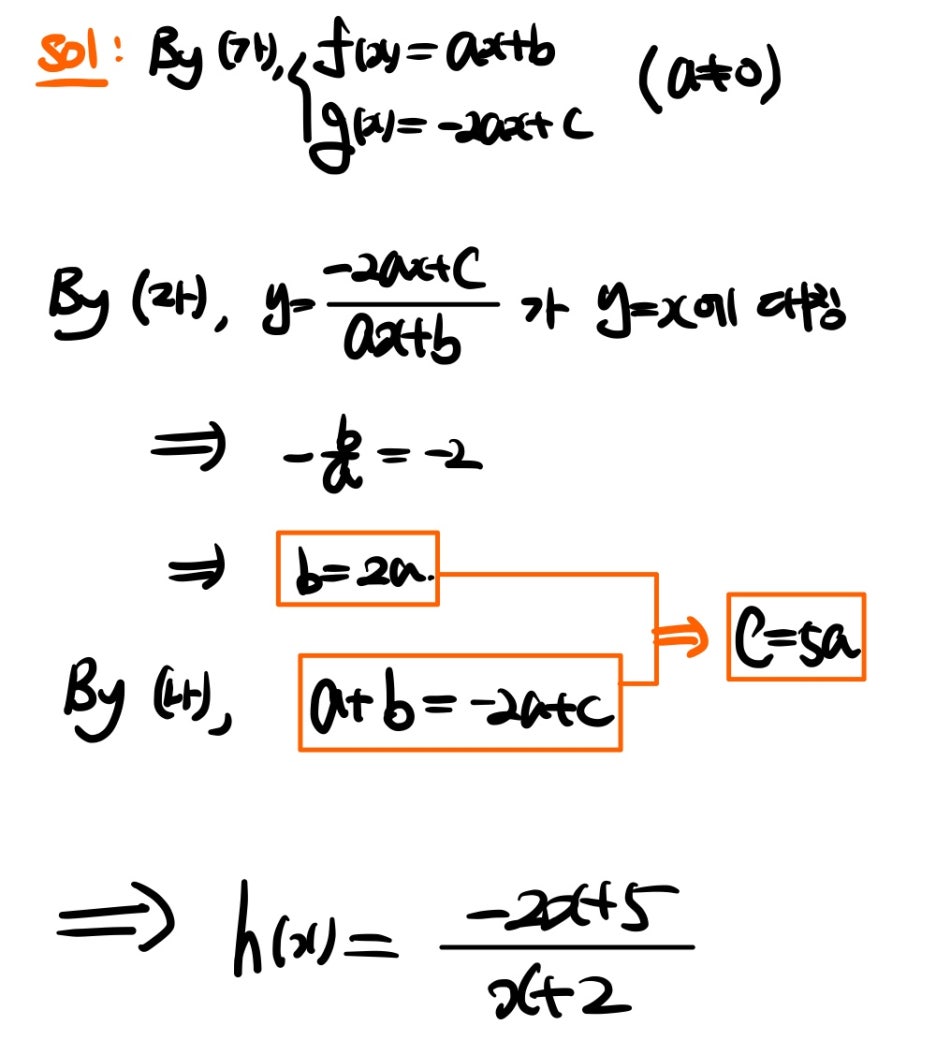
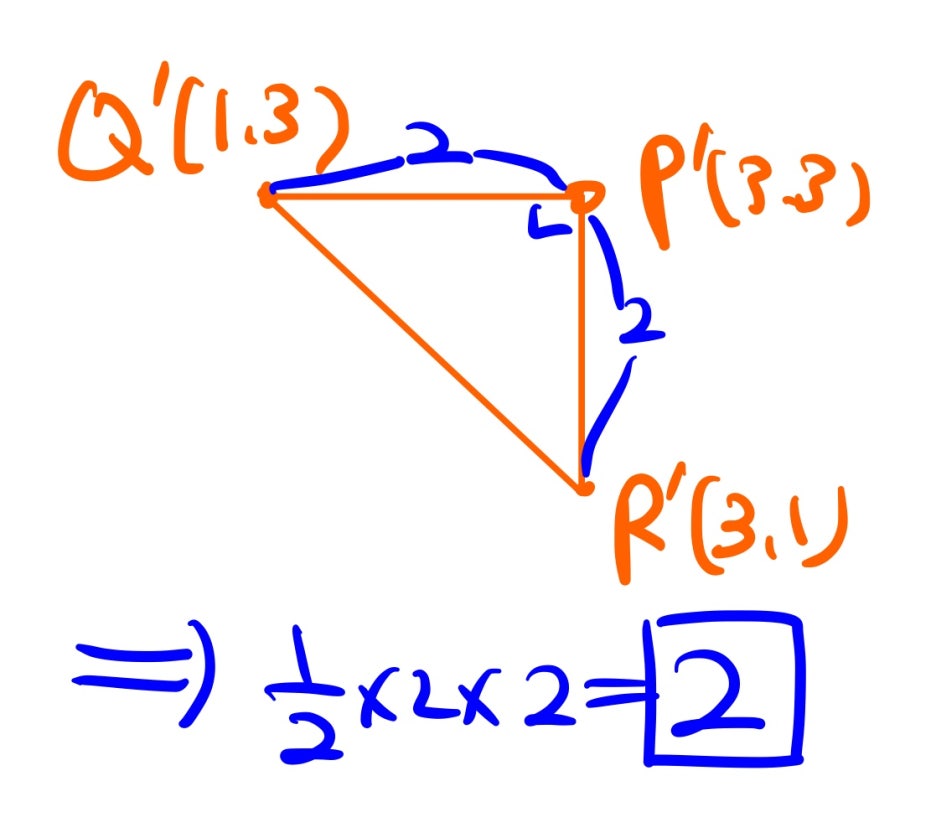
이제 삼각형의 넓이가 최소인 경우를 생각하면 되는데, 계산의 편의를 위해 저는 다음과 같이 평행이동을 했습니다.
평행이동을 해도 삼각형의 넓이는 변하지 않으니 PQR=P'Q'R'이겠죠?
그런데 P'Q'R'의 넓이가 최소가 되는 것은 점 P'에서 선분 Q'R'에 내린 수선의 길이가 최소일 때 입니다. 왜냐하면 이것이 직각이등변삼각형이기 때문입니다!ㅎㅎ
a=3일 때, 삼각형 P'Q'R'의 넓이가 최소이므로~ 이때 넓이를 구하면 되겠죠? 따라서 답은 다음과 같습니다.
기계적으로 문제와 그 풀이를 암기하는 방식으로 공부한 학생이라면 위 세 문항에서 크게 당황 했을 수도 있을 것 같습니다. 하지만 위의 풀이처럼 차근차근 풀면 "[과천중앙고] 2023년 1학년 2학기 기말고사"도 별로 어렵지 않죠?
기계적으로 문제 풀이를 하는 학생을 우수한 학생이라고 생각하는 대학은 없습니다. 배운 것에 근거해서 논리적으로 문제를 해결함으로써 실력을 쌓아나감으로써 우수한 학생이 된다면, 최상위권 대학에서도 여러분을 선발하고자 노력할 거에요. 그러니 그냥 열심히'만' 공부하지 말고, 실력이 쌓이는 방법으로 노력하길 바랍니다!
다음은 실력이 쌓이는 공부 방법에 대한 포스팅 및 전자책 링크입니다.
1. 고난도 문항 치트키 1
2. 고난도 문항 치트키 2
4. 서울대 박사가 알려주는 수학의 비밀 - 첫 번째 비밀 : 집합
5. 서울대 박사가 알려주는 수학의 비밀 - 두 번째 비밀 : 명제
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
사실 논술 준비는 거의 못했단 말이죠 확실히 최저도 못맞출거같을 때 & 확실히...
-
내신은 8학군 2점대 극초반이고 정시파이턴데 설의 설치 같은 곳은 세특을 따로...
-
수특은 KBS듣는중인데 수완 어카지 책 사놨는데 못풀거같음.... 어카지 수특도 다 안끝났는데 ㄹㅇ
-
진짜 거의 다왔다 ㅋㅋ
-
아바라는 컴포즈가 압승인듯 아아도
-
실모안치고 일희일비중 막 자신감 개떨어졌다가 자신감 갑자기 생기고 그럼 ㅋㅋㅋ
-
-
?
-
설맞이 풀어보고 싶은데 지금 시기에 푸는거 에바임? 1
설맞이 아카이브나 모의고사 풀어보고 싶은데 지금 사서 풀어도 안늦을까요?
-
사문 질문 1
지속적인 경기 불황으로 일자리가 감소하자 독거노인의 생계형 범죄가 늘어나는 경우는...
-
2합4 영어사문 0
최저 맞춰야하는데 지금 사문 2 영어 2 생각하고 있어요.. 영어가 안정 1은 항상...
-
국어 실모 0
이감6-10 key모 상상 9,10 네 개있는데 오늘 키모 풀고 두 개 더 풀...
-
뭐들을까요
-
진짜 국밥에 당면만 있는 순대를 넣나요? 그 쫜득거리는
-
무슨강의 몇강인지좀알려주세여ㅠ
-
5000부 판매돌파 지구과학 30분의기적 파이널 총정리집을 소개합니다. (현재...
-
멱집합 이진수 개어려운데.. 이해가 안 됨
-
고전소설 비연계 고전시가 비연계 극 연계 때리는게? 이감의 깊은 뜻인가
-
메가 대성 2
둘 다 사는거 ㄱㅊ은 선택이겠죠 한지 사문인데 이기상이 너무 듣고싶어요 원래 대성만 하는데
-
긴장되는거 쫄리는거 전혀 없고 그냥 결과가 어떻든 빨리 끝났으면 좋겠음 당장...
-
엄마가 나에 대한 기대를 품게 만들지만 않았어도 내 10대는 행복했을텐데
-
쿠팡 좋네 0
ㄹㅇ 신세카인데....
-
ㄴ 선지에서 왕안석이 틀린 이유를 어떻게 판다해야 하나요? 216해설강의를 보면...
-
가채점표 안쓸듯 2
가채점표 겁나 사놨는데 걍 수험표에 표 그려서 바로 갈기는게 시간 덜걸리는거같음...
-
로피탈 질문 4
이거 맞나여??
-
이 다음에 뭐 푸시나요?
-
-
소설도 막 미친듯이 못알아먹게 모르는 단어 남발 아니면 어느정도 읽히는데 고전시가나...
-
조퇴하고 병결해야하나
-
1. 올해 서울대 가려는 친구들은 가산점 때문에 2과목 2개하나요? 작년엔 2랑...
-
콘서타27 매일 복용하고 평가원 모고때는 긴장을 심하게 해서 위부팽만감 + 심장이...
-
ㄱㄱ
-
입실하러 가기 전에 집에서 싸고 가고 싶은데 집에서 한번 싸도 국어나 수학 볼때 꼭...
-
뭐든 상관 없으니 그냥 공감해줘.
-
지금 ㄹㅈㄷ로 조용하네 내일부터 8 40에 쳐야겠다
-
오밐추 3
오부이들 오늘도 화이팅
-
[속보] CNN 초기 출구조사, 후보 긍정적 평가 해리스 46% vs 트럼프 42% 3
후속기사가 이어집니다
-
제발요 너무졸림
-
국어 : 구주 연마의 서 복습 + 최근 3개년 수능 + 언매 기출 + 혜윰 모의고사...
-
성적차이 말 안 됨
-
내일부터 기출로 회귀해야지
-
부사관 학벌 2
대부분 고졸 혹은 지방 4년제 맞음??
-
-
오늘의 모닝실모 1
한수 8회 강대X 10회 목표 점수대 90이상 100이상
-
강의실 책상에 그대로 있네 진짜 존나 다행이다
-
옯모닝 0
음 9시이전이면 얼버기지.. 음음
-
수 상 수 하 개념을 아예 모르는 건 아니지만 내신공부를 하나도 안했다보니 문제를...
-
다들 화이팅!
-
와 1
수능 냄새 난다
-
동네 작은 학원에서 재수반 관리 및 수학을 가르치는 강사입니다 오늘 모의고사 치르는...
아, 참고로 14번 문항은 오류입니다. (k=-5이면 상수함수가 돼서 ㄱ, ㄴ, ㄷ가 모두 거짓이 됩니다^^;;) 집합에서 구별법을 공부해야 한다고 강조했는데~ 분수함수인지 아닌지 구별하는데 신경을 안 쓴 것이 오류의 원인이 된 듯 합니다.